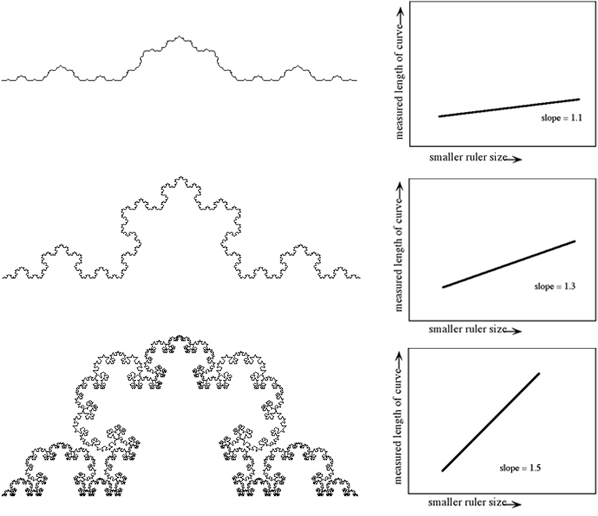
As we shrink down the ruler size, the length increases to infinity. But how fast does it increase? For a smooth Koch curve, it increases slowly. For a rough one it increases quickly. The slope of the line tells you how fast or slow. It is the fractal dimension.

A line has one dimension, a square 2, But fractals are in-between, so they have a fractional dimension! That is how they can fit infinity into a finite space. Their curve is so torturous that it is more than one dimensional. In fact it can get so wiggly that it actually does become a space-filling curve, in which case the fractal dimension will be 2.0 (a surface!).